一、问题描述
这是我之前工作中遇到的一个问题。一个粗粒度服务由若干细粒度服务构成,这些细粒度服务在执行过程中有可能并行,有可能串行,每个细粒度服务都一定的执行时间,这些执行时间都会写入数据库中。试设计算法统计一个粗粒度服务的执行时间。
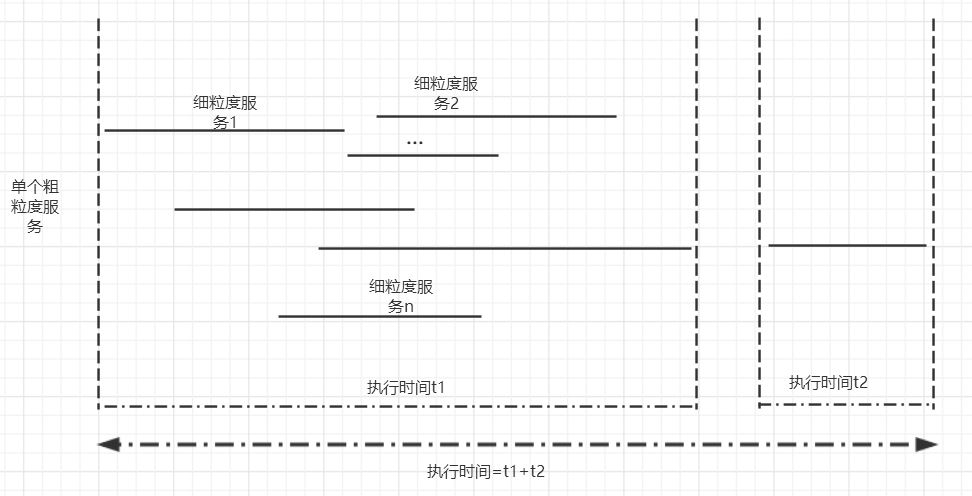
图1.问题示例。
如图1.一个粗粒度服务由若干细粒度服务组成,这些细粒度服务有可能交叉重合也有可能完全不重合。求粗粒度服务的执行时间就等于所有细粒度服务从开始执行,到执行结束,实际占有的时间片段之和(有点拗口)。简单说就是,该粗粒度服务执行的时间范围内,如果某个时刻有至少一个该服务的子服务(细粒度服务)执行,那么就认为该服务是执行的,否则则不计算在内(比如图1.所示,执行时间t1和t2之间的时间段就不算作执行时间)。
二、实现思路
乍看之下,时间段跟时间段彼此搅在一起,要把它们的执行时间求出很不容易。这时我的想法是,先从最简单的二元关系进行考虑。任何两个时间段的关系都可以分为如下这六种关系。
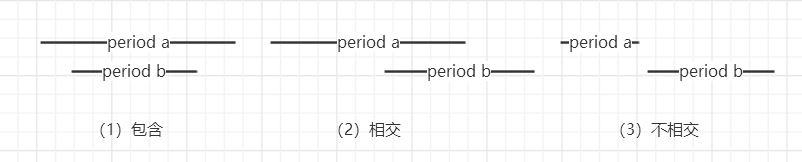
图2(a).时间片段a和b的三种关系。

图2(b).时间片段a和b的另外三种关系。
如图2(a),我们可以看到时间片段a和b分别对应了包含,相交和不相交这三种关系。但同时,根据对称性,我们又得到图2(b)。实际上,我们可以让图2(b)的情形等价于图2(a),只需让时间片段a和b的身份互换即可。
值得注意的是图2(a)中,时间片段a的起始时刻都早于时间片段b的起始时刻,因此我们如果按起始时刻将所有的时间片段进行排序,那么相邻两两之间的时间片段计算就都统一为图2(a)中的三种情况了,这样就大大简化了问题的复杂度。
三、算法实现
3.1 算法一:逐一合并算法
3.1.1 算法描述
如图3.我们先将所有的时间片段按照起始时刻排序,后面的处理过程即依次判定相邻两个时间片段的三种关系,并将统计时间进行合并,合并的时间片段可以作为一个新的时间片段与后继的时间片段进行相关的计算。
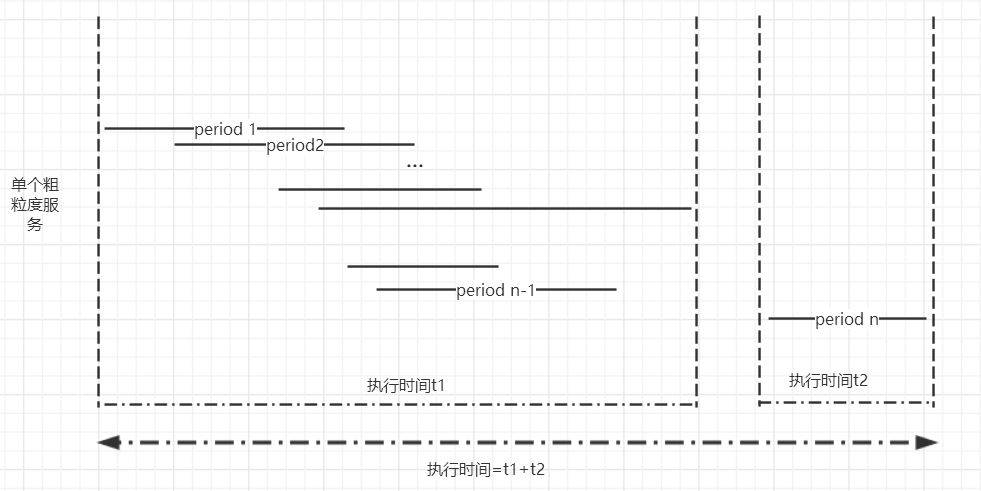
图3.新的时间片段统计算法。
算法部分总共分两步,
一,将时间片段按开始时间进行排序,这里可以使用冒泡或快速排序算法。
二,1. 从第一个时间片段period 1开始,与后面的period 2 进行比较,取二者的并集,得到的新的period 2’。
2.重复上面的过程,直到最后一个时间片段并入最终的时间片段为止。
3.1.2 算法实现
为方便这里将时间都统一处理为long型,事实上,计算时间差也的确需要取date类型数据的long值再进行相关计算。


package com.example.demo.mine.time_collect;import java.util.*;import lombok.Data;import lombok.extern.slf4j.Slf4j;/** * * @author lunyu * @since 2018-03-03 */@Slf4jpublic class StatisticTime { public static void main(String[] args) { // 1.产生随机数据 int size = 10; List periods = new ArrayList ();// long currentTime = System.currentTimeMillis(); //不失准确性,可以设当前时间是0 long currentTime = 0; int range = 100; int start; int end; int coi; Random random = new Random(); for (int i = 0; i < size; i++){ //区间膨胀系数 coi = random.nextInt(9)+1; start = random.nextInt(range*coi); end = random.nextInt(range*coi) + start; Period period = new Period(currentTime + start, currentTime + end); log.info("时间片段:{}-{}", period.getStartTime(), period.getEndTime()); periods.add(period); } //2.算法执行 //2.1先对各个时间段按开始时刻进行排序 sortPeriodsByStartTime(periods); //2.2对数据统计 long totalSpendTime = statisticTime(periods); log.info("总用时:{}", totalSpendTime); } /** * 对排序后的数据进行统计 * @param periods * @return */ private static long statisticTime(List periods) { long sum = periods.get(0).getEndTime() - periods.get(0).getStartTime(); for(int i = 0; i < periods.size() - 1; i++) { //1.如果(period i) 和(period i+1)相交,例: // ------------ // --------- if (periods.get(i).getEndTime() > periods.get(i + 1).getStartTime() && periods.get(i).getEndTime() < periods.get(i + 1).getEndTime()) { sum += periods.get(i + 1).getEndTime() - periods.get(i).getEndTime(); //2.如果(period i) 和(period i+1)不相交,例: //----------- // ------ }else if (periods.get(i).getEndTime() <= periods.get(i + 1).getStartTime()) { sum += periods.get(i + 1).getEndTime() - periods.get(i + 1).getStartTime(); //3.如果(period i) 包含(period i+1),例: //--------------- // ----------- }else if (periods.get(i).getEndTime() >= periods.get(i + 1).getEndTime()) { //这时什么都不做,因为(period i) 所对应的长度即为(period i) 和(period i+1)并集的时间长度。 //sum +=0; } } return sum; } /** * 对时间段按开始时间进行顺序排序,简单起见,用冒泡算法 * @param periods */ private static void sortPeriodsByStartTime(List periods) { //冒泡法,从后向前冒泡 for(int i = periods.size() - 1; i > 0; i--) { for(int j = periods.size() - 2; j >= 0; j--) { if (periods.get(j).getStartTime() > periods.get(j+1).getStartTime()) { swap(periods, j, j+1); } } } } /** * 交换对象 * @param periods * @param j * @param i * @return */ private static void swap(List periods, int j, int i) { Period tempPeriod = new Period(0, 0); tempPeriod = periods.get(j); periods.set(j, periods.get(i)); periods.set(i, tempPeriod); } /** * 区间对象 * @author lunyu * @since 2018-03-03 */ @Data private static class Period{ public Period(long startTime, long endTime) { super(); this.startTime = startTime; this.endTime = endTime; } /** * 开始时间 */ private long startTime; /** * 结束时间 */ private long endTime; }} 不难知道算法的空间复杂度为O(1),时间复杂度为O(n2) (排序冒泡算法复杂度:O(n2) + 时间片段并集计算复杂度:O(n))。
3.2 算法二:化整为零算法
3.2.1 算法描述
将每个时间片段的端点,都取出,并排序,我们就得到了n个细粒度服务分割的2n个时间点。
如图所示蓝色虚线与时间轴的交点表示每个时间端点,这些端点分割了时间从t1,t2一直持续到t2n。
将这些区间段分别与每个细粒度服务的时间片段进行比较,如果在某个细粒度服务的时间片段内,那么我们认为该时间段为执行时间。
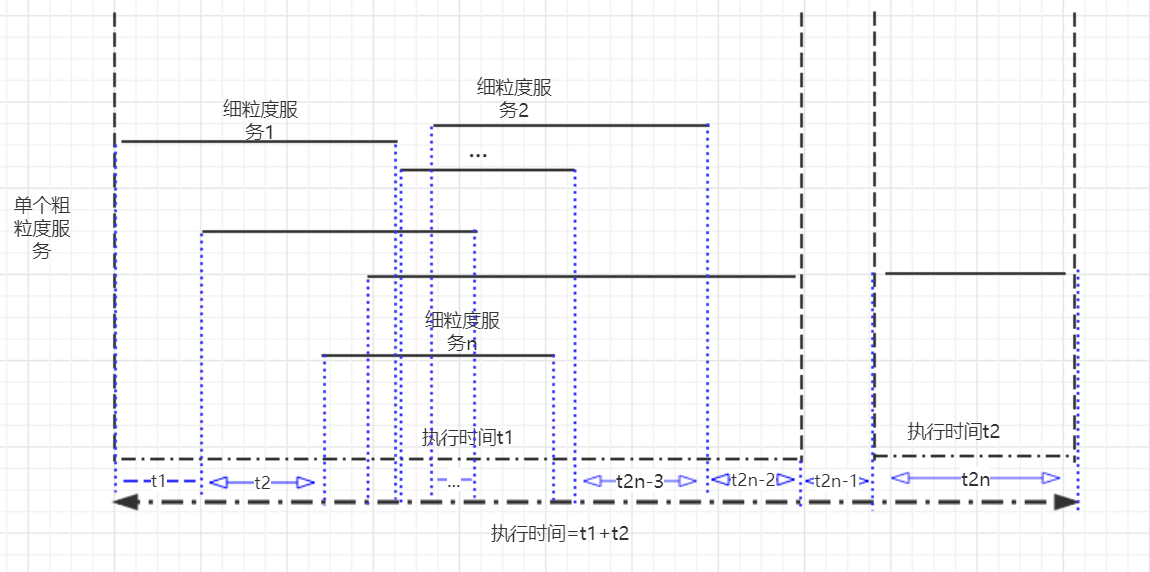
图4.细粒度服务端点对时间的分割。
3.2.2 算法实现


import com.google.common.collect.Lists;import java.util.ArrayList;import java.util.List;import java.util.Random;import lombok.Data;import lombok.extern.slf4j.Slf4j;/** * 化整为零的方式处理代码 * @author lunyu * @since 2018-03-03 */@Slf4jpublic class StatisticTimeByAll2Part { public static void main(String[] args) { // 1.产生随机数据 int size = 10; List periods = new ArrayList ();// long currentTime = System.currentTimeMillis(); //不失准确性,可以设当前时间是0 long currentTime = 0; int range = 100; int start; int end; int coi; Random random = new Random(); for (int i = 0; i < size; i++){ //区间膨胀系数 coi = random.nextInt(9)+1; start = random.nextInt(range*coi); end = random.nextInt(range*coi) + start; Period period = new Period(currentTime + start, currentTime + end); log.info("时间片段:{}-{}", period.getStartTime(), period.getEndTime()); periods.add(period); } //2.算法执行 //2.1 获取所有的时间点集合 List allTimePoints = getAllTimePoints(periods); //2.2 对所有的时间点集合进行排序 sort(allTimePoints); //2.2对数据统计 long totalSpendTime = statisticTime(allTimePoints, periods); log.info("总用时:{}", totalSpendTime); } private static long statisticTime(List allTimePoints, List periods) { long totolSpendTime = 0; for (int i = 0; i < allTimePoints.size() -1; i++){ long startTimePoint = allTimePoints.get(i); long endTimePoint = allTimePoints.get(i + 1); //对时间进行验证 for (Period period : periods){ //如果某个(细粒度)时间片段包含该分割的时间片段,则认为分割的时间片段执行时间 if (startTimePoint >= period.getStartTime() && endTimePoint <= period.getEndTime()){ totolSpendTime += (endTimePoint - startTimePoint); break; } } } return totolSpendTime; } /** * 为简单起见,用冒泡法对时间点进行排序 */ private static void sort(List allTimePoints) { //冒泡法,从后向前冒泡 for(int i = allTimePoints.size() - 1; i > 0; i--) { for(int j = allTimePoints.size() - 2; j >= 0; j--) { if (allTimePoints.get(j) > allTimePoints.get(j+1)) { swap(allTimePoints, j, j+1); } } } } /** * 交换对象 * @param allTimePoints * @param j * @param i * @return */ private static void swap(List allTimePoints, int j, int i) { long tempPeriod = allTimePoints.get(j); allTimePoints.set(j, allTimePoints.get(i)); allTimePoints.set(i, tempPeriod); } /** * 获得所有的时间点 * @param periods * @return */ private static List getAllTimePoints(List periods) { List allTimePoints = Lists.newArrayList(); for (Period period : periods){ allTimePoints.add(period.getStartTime()); allTimePoints.add(period.getEndTime()); } return allTimePoints; } /** * 区间对象 * @author lunyu * @since 2018-03-03 */ @Data private static class Period{ public Period(long startTime, long endTime) { super(); this.startTime = startTime; this.endTime = endTime; } /** * 开始时间 */ private long startTime; /** * 结束时间 */ private long endTime; }} 不难知道,需要一个list用以保存2n各时间端点,因此,该算法的空间复杂度为2O(n)。对2n个时间端点进行排序,其时间复杂度为4O(n2),每个分割的时间段与细粒度服务的时间段比较,最多比较2n*n次,其时间复杂度为O(2n2),因此总的时间复杂度为4O(n2)。
四、问题的推广
4.1 二维覆盖的情况
4.1.1 问题分析
为简单起见,这里只考虑矩形覆盖的问题。

图4. 随机分布的矩形及其覆盖。
如图,左侧是一系列随机的矩形,这些矩形可能相交,也可能不相交,我们的目的是求这些矩形覆盖的面积(右侧)。
说说问题的复杂性,这个问题本来我想用一维时间段的方式拓展到二维来处理。发现,实际上行不通。因为,二维矩形图形之间的关系不能简单划归为两个矩形之间的关系。首先图形间的关系是一种偏序关系,即按照x轴的顺序是acb但是按照y轴的顺序是abc,如图5。
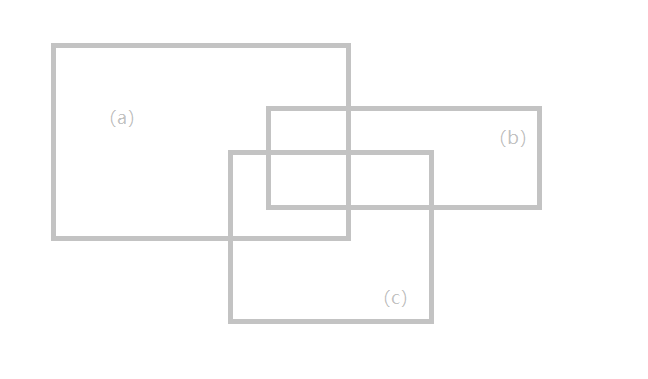
图5.三个矩形的某种分布。
这样就会造成如下问题:
- 当进行面积计算的时候,随着矩形块的增加,数据的计算会越来越复杂,也就是不能像之前一样排序之后,数据可以化归到更简单的二元形式。比如上图,把a和b矩形合并后,再与c进行面积运算的时候,必须要同时计算a-c,b-c的关系。
- 矩形不能随意的移动,比如a-c间的关系,两者的关系是固定的,不能随意移动。
由于上述问题的存在,目前能想到的解决方案即通过3.2算法二(化整为零算法)的方式来解决。
4.1.2 算法描述
算法如下:
- 统计所有的矩形组成的A集合中矩形的横坐标和纵坐标,并将横坐标和纵坐标进行排序。
- 依次取相邻的横坐标,相邻的纵坐标,相邻的横坐标和相邻的纵坐标这样可以组成一个个小的矩形集合B。
- 依次对矩形B集合中元素b与矩形A集合中a进行比较,如果矩形b包含于矩形a,则加上矩形b的面积,否则,跳过。
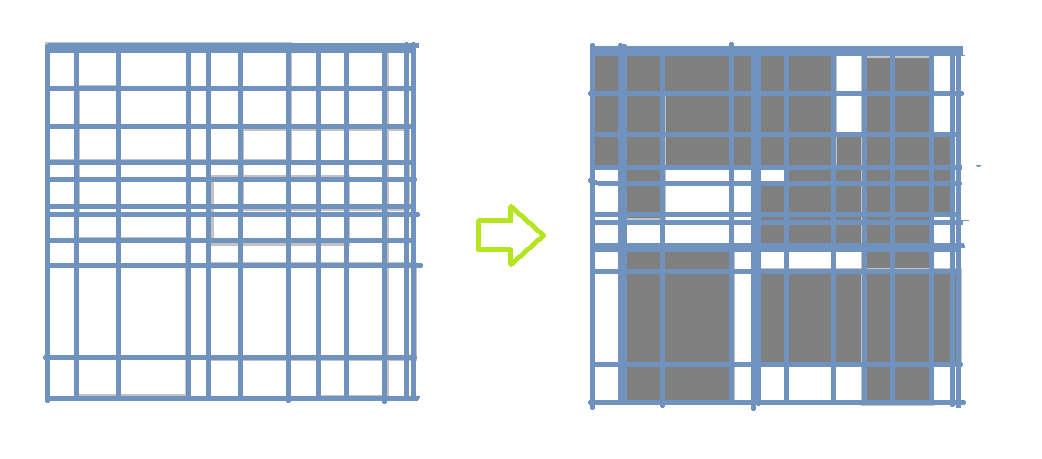
图6. 横坐标纵坐标对图形区域的分割和覆盖。
如图6,蓝色的线将矩形块,分割成一块块更小的矩形区块,求覆盖的区块所占的面积就可以对这些小区块分别判定求和。
4.1.3 算法实现


import com.google.common.collect.Lists;import java.math.BigDecimal;import java.util.Collections;import java.util.List;import java.util.Random;import lombok.AllArgsConstructor;import lombok.Data;import lombok.experimental.Accessors;import lombok.extern.slf4j.Slf4j;/** * 面积统计 */@Slf4jpublic class AreaStatisticByAll2Part { public static void main(String[] args) { // 1.产生随机数据 int size = 2; int range = 100; int xLeft; int xRight; int yLower; int yUpper; int coi; Random random = new Random(); List rectangleList = Lists.newArrayList(); for (int i = 0; i < size; i++){ //区间膨胀系数 coi = random.nextInt(9) + 1; xLeft = random.nextInt(range*coi); xRight = random.nextInt(range*coi) + xLeft; coi = random.nextInt(9) + 1; yLower = random.nextInt(range*coi); yUpper = random.nextInt(range*coi) + yLower; Rectangle rectangle = new Rectangle(xLeft, xRight, yLower, yUpper); log.info(rectangle.toString()); rectangleList.add(rectangle); } //1.将横坐标和纵坐标的数据分别装载并进行排序 List xAxes = getXAxes(rectangleList); List yAxes = getYAxes(rectangleList); Collections.sort(xAxes); Collections.sort(yAxes); //2.对数据进行比较 BigDecimal areaSum = compareAndGetAreaSum(xAxes, yAxes, rectangleList); log.info("总面积:{}", areaSum.toString()); } /** * 比较并获得面积 */ private static BigDecimal compareAndGetAreaSum(List xAxes, List yAxes, List rectangleList) { BigDecimal areaSum = BigDecimal.ZERO; for (int i = 0; i < xAxes.size() -1; i++){ int xLeft = xAxes.get(i); int xRight = xAxes.get(i + 1); for (int j = 0; j < yAxes.size() -1; j++){ int yLower = yAxes.get(j); int yUpper = yAxes.get(j + 1); for (Rectangle rectangle : rectangleList){ if (xLeft >= rectangle.getXLeft() && xRight <= rectangle.getXRight() && yLower>= rectangle.getYLower() && yUpper <= rectangle.getYUpper()){ areaSum = areaSum.add(BigDecimal.valueOf((xRight - xLeft) * (yUpper - yLower))); break; } } } } return areaSum; } /** * 获得所有的Y轴坐标数据 */ private static List getYAxes(List rectangleList) { List yAxes = Lists.newArrayList(); for (Rectangle rectangle : rectangleList){ yAxes.add(rectangle.getYLower()); yAxes.add(rectangle.getYUpper()); } return yAxes; } /** * 获得所有的X轴坐标数据 */ private static List getXAxes(List rectangleList) { List xAxes = Lists.newArrayList(); for (Rectangle rectangle : rectangleList){ xAxes.add(rectangle.getXLeft()); xAxes.add(rectangle.getXRight()); } return xAxes; } /** * 矩形实体 */ @Data @AllArgsConstructor @Accessors(chain = true) public static class Rectangle { private Integer xLeft; private Integer xRight; private Integer yLower; private Integer yUpper; }} 不难知道,算法的空间复杂度是 4O(n)(用以存储横坐标和纵坐标的空间是2n+2n=4n个),时间复杂度是4O(n3)(排序的时间复杂度O(n2)(以冒泡算法为例) ,循环比较的次数为2n*2n*n=4n3次)。
4.2 三维及以上的情形
可以以此类推,将三维或更高纬度的空间分割成一个个小的空间,将这些空间一一与随机分布的立方体(或超体)进行比较,比较的结果并统计最终结果。不难知道,k维的情形,算法的空间复杂度是O(2kn),算法的时间复杂度是O(2(k-1)nk)。